

Copyright ©2019 Thomas Schwengler. A significantly updated and completed 2019 Edition is available.
Large scale fading, or shadowing is fading that occurs on several meters or more; it reflects conditions that may vary as one turns a corner, moves behind a large building, or enters a building.
Large-scale variations caused by shadowing of obstacles are shown to follow a log-normal distribution [17][18][19]; which means that, when shadowing power levels are measured in dB, they follow a Gaussian distribution. Consequently, shadowing effects they are usually incorporated into path loss estimates by the addition of a zero-mean Gaussian random variable, with standard deviation σ: N(0,σ), were σ is often estimated by empirical measurements. Commonly accepted values for σ are between 6 dB and 12 dB.
Measured values of σ itself seem to display Gaussian distribution as well, in their variations from one area to another, and depend on: the radio frequency, the type of environment (rural, suburban, or urban), base station and subscriber station height. Many measurement campaigns have been conducted and reported in the literature, some of which are summarized in table 4.1.
| Source | Frequency | Path Loss | σ | Comments |
| (GHz) | Exponent n | (dB) | ||
| Seidel [69] | 0.9 | 2.8 | 9.6 | Suburban (Stuttgart) |
| Erceg [32] | 1.9 | 4.0 | 9.6 | Terrain-category B |
| Feuerstein [70] | 1.9 | 2.6 | 7.7 | Medium antenna height |
| Abhayawardhana [71] | 3.5 | 2.13 | 6.7–10 | [71] Table 2, 3. |
| Durgin [72] | 5.8 | 2.93 | 7.85 | [72] Fig. 7, residential |
| Porter [73] | 3.7 | 3.2 | 9.5 | Some denser urban |
| Rautiainen [74] | 5.3 | 4.0 | 6.1 | [74] Fig. 3, 4. |
| Schwengler [75] | 5.8 | 2.0 | 6.9 | LOS |
| 5.8 | 3.5 | 9.5 | NLOS | |
| 3.5 | 2.7 | 11.7 | Near LOS | |
| Average | 3.5-5.8 | 3.0 | 8.7 | |
| 0.9-1.9 | 3.1 | 9.0 | ||
| Approximation | 1-6 | n = 3.0 | σ = | 9.29 - 1.58log(fGHz) |
To describe a wireless link, one we often seek to establish link budgets: they provide detailed power information from transmitter to receiver; but they provide only a median value for these power levels, actual levels vary with many other parameters, including shadowing.
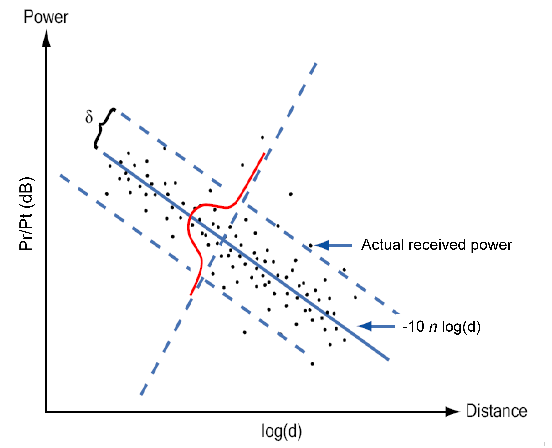
Usually a minimum signal strength is required to maintain service. In order to maintain signal strength above that level, an additional margin is added to the link budget. Jakes’ equation [76] gives an estimate of such excess margin, or fade margin. The assumption is that the shadowing statistic throughout the cell is log-normally distributed (i.e. values in dB are normally distributed):
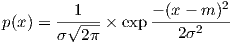 | (4.1) |
Copyright ©2019 Thomas Schwengler.
The probability that x exceeds the threshold x0 (the receiver threshold that
provides an acceptable signal) at a given radius R is
![∫ ∞
P (R ) = P [x ≥ x ] = p(x)dx
0 0 x0](classweb91x.png) | (4.2) |
By integrating the probability density function from x0 to ∞, the edge reliability result is
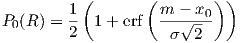 | (4.3) |
Typically the threshold of interest x0 is lower than the median provided by the path loss model, and the value m-x0 is an excess, positive amount (in dB), and is usually referred to as excess margin, or fade margin: F = m - x0. Of course, for a fade margin of zero (m - x0 = 0) at a given R, the error function (erf) equals zero, resulting in 50% edge reliability.
Alternative representations of that formula sometime make use of the complementary error function or the Q function. 1
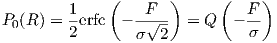 | (4.4) |
Instead of an edge reliability, the reliability in the entire cell area is often more useful: the fraction of useful service area, FA(R), within a circle of radius R where the received signal strength exceeds a threshold value x0 is the integration of the probability function over the area as shown below.
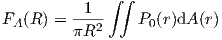 | (4.5) |
With the assumption that the mean value of the signal strength, m, behaves
according to an r-n propagation law, then m = mR - 10nlog 10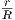 , where n is the
propagation exponent value; and mR (in dB) is the mean signal strength at the
edge distance r = R (mr is determined from the transmitter power, antenna
heights, gain, and so on), thus the value mR -x0 in equation (4.6) corresponds to
the excess margin at the edge). Substituting m into the probability density
function gives the area reliability: (after substitution and integration by
part):
, where n is the
propagation exponent value; and mR (in dB) is the mean signal strength at the
edge distance r = R (mr is determined from the transmitter power, antenna
heights, gain, and so on), thus the value mR -x0 in equation (4.6) corresponds to
the excess margin at the edge). Substituting m into the probability density
function gives the area reliability: (after substitution and integration by
part):
![[ ( ) ( )]
FA (x0,σ) = 1-1 - erf(a) + 1 - erf1--ab- exp 1--2ab-
2 b b2](classweb100x.png) | (4.6) |
where
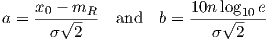 | (4.7) |
where x0 - mR is simply the opposite of the excess margin at the edge.
Link budgets are a convenient tool to compare power levels between different technologies and different systems. Terrain conditions for instance may cause great variations in how far a wireless system reaches; link budgets allows for good system comparison while removing some of these variations.
Copyright ©2019 Thomas Schwengler. Significantly updated and completed in 2019 Edition available here.
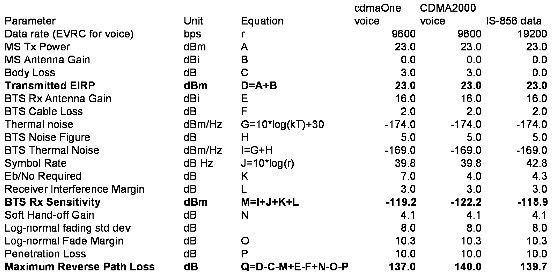
We will examine link budgets for popular new wireless access standards such as cdmaOne (IS-95), cdma2000 (IS-2000), EV-DO (IS-856) [81], and fixed WiMAX. We will also discuss coverage and capacity tradeoffs, increasing throughput vs. capacity or coverage, soft handoff benefits and cost.
Link budgets from different radio manufacturers are sometimes difficult to compare because they use different terms and definitions (without always clearly specifying them). Always compare them to a common definition, and try to identify the following parameters.
ERP is smaller than EIRP by the amount of gain difference between an isotropic antenna and a dipole, that is 2.15 dB. (Indeed a dipole gain is 0 dBd=2.15 dBi, so any antenna gain G may be expressed in either unit with the simple conversion G(dBi) = G(dBd) + 2.15 dB, and EIRP=ERP+2.15 dB.)
Some care must be taken to define the receiver sensitivity, which is the lowest power level at which the received signal may be decoded, it is usually defined as a power level above ambient noise and interferences, and depends on several parameters such as bit rate, coding, error rate. It uses the following parameters:
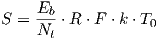 | (4.8) |
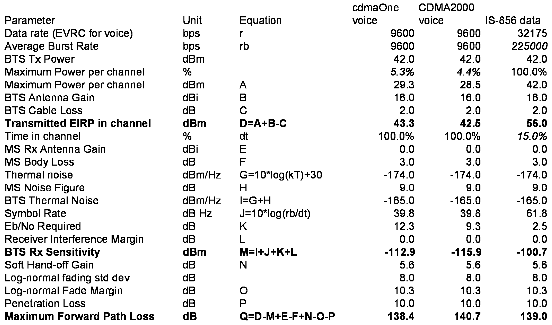
Other similar and equivalent expressions my be derived for system sensitivity using the minimum SNR required in an RF channel or bandwidth B, in which case S = SNR ⋅ F ⋅ Nt or:
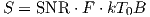 | (4.9) |
(as seen in link budget on figure 4.5).
Different manufacturers present link budgets differently, and some analyses are required to reduce them to a common format. Still, transmitted EIRP, receiver sensitivity, excess margin, and maximum allowable path loss can usually be found.
Equipment manufacturers typically claim a certain reverse link budget, which is studied by potential operator buyers in order to predict performance, coverage, capacity, and compare them with other equipment vendors. The reverse link lends itself well to a straightforward power budget, based on the mobile maximum transmit power and the base sensitivity level and the industry commonly admits that reverse link budgets are the basis for radio design, and the forward link is studied subsequently, simply in order to verify that it provides enough resources to be balanced with the reverse link.
Equipment manufacturers sometimes do not provide forward link budgets, and argue that systems are usually reverse-link limited. For voice systems, both reverse and forward link budgets should be balanced; the forward link budget should insure that a power allocation between devices within the cell is sufficient to provide enough capacity. For data systems, the revers link is typically used to define a maximum range, and the forward link allows to determine the corresponding download speeds.
Unlike in the reverse link, the entire power is not necessarily allocated to one remote client device: either a portion of orthogonal channels (CDMA or OFDMA) are allocated to it, or a certain percentage of the time (as in TDMA, or IS-856 EV-DO). The link budget should reflect that fact as shown on forward link budget figures of this section. (The details of derivation of these percentages are not trivial and depend heavily on standards, system efficiency, and suppliers implementations.)
There are several differences between voice an data link budgets. Voice SNR requirements are typically higher, as higher data rates can benefit from increased coding efficiency (like turbo-coding) and is less delay-sensitive and can afford some retransmit. For instance a cdma2000 link budget for EVRC voice (9.6kbps) requires an Eb/No value around 4 to 5dB, which I can achieve a data rate around 38.4kbps (thanks to more efficient coding and retransmissions).
Data link budgets vary greatly with data rates, so it is important to specify the data rate expected given a certain channel bandwidth, modulation, and coding. Finally body loss (usually 3 dB) associated with the handset near the head (or on the belt with a hands-free device) are usually omitted (of course this is somewhat debatable as the data device is still near the human body).
Wireless standards that allow multiple bandwidth, such as LTE, have to specify the bandwidth used for the link budget (either in MHz, of in number of resource elements detailed further in §8.3). It is always important to specify how much spectrum is used (or how many resource blocks) for what data rate.
Whenever possible, operators use licensed spectrum for wireless communications. For instance CDMA systems are commonly used at PCS frequency (1.9 GHz), and fixed WiMAX systems operate at 3.5 to 3.7 GHz. We summarize parameters for these licensed radio systems with the link budgets shown on figures 4.2 to 4.4.
Link budgets in unlicensed bands are similar to the above but are usually limited by a lower maximum allowed EIRP set by government regulations (FCC in the US) as shown in a separate table on figure 4.5.
We’ve seen in §3.3 the impact of multiple rays on propagation models: this effect of multipath causes deep fades within small distances and is referred to as small-scale fading. Another important yet different cause of fading is that of small frequency variations such as Doppler effect. Both of these small-scale fading effects are studied in this section. 2
Multipath fading is significant for both mobile and fixed wireless systems. Intuitively that type of fading varies with surrounding scatterers which reflect differently the wavefront between transmitter and receiver. Practically, it is very important to quantify that aspect of the propagation environment, and even to taylor the standard to perform well in such an environment: for instance we’ll see later that the length of a transmitted symbol will be depending on the multipath situation in which it has to perform well.
In the time domain, multipath parameters can be seen as the spread of the arriving waves. In the frequency domain, the concept is less intuitive and relates to a coherence bandwidth, that is the width of the spectrum that is attenuated by a fade. The main parameters are summarized in table 4.2.
| Multipath | Parameter | Symbol |
| Time domain | Channel impulse response | H(t) |
| Mean excess delay | ||
| RMS delay spread | στ | |
| Excess delay spread | τX | |
| (for x dB threshold) | ||
| Frequency domain | Channel impulse response | H(f) |
| Coherence bandwidth (90%) | Bc ≈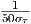 |
|
| Channel impulse response (50%) | Bc ≈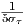 |
|
Flat or frequency-selective fading: Depending on the values of these above parameters and how they compare to the speed of transmitted symbol, the wireless channel will have flat fading (over the entire bandwidth used) or frequency-selective fading. This is of course a frequency domain interpretation describing what happens to the signal: it is either faded over the entire spectrum, or selectively only over a portion of it.
High or low delay spread: Again depending on the values of the above parameters and how they compare to the length of transmitted symbol, the wireless channel is said to have high delay spread (or heavy multipath), or low delay spread (low multipath). This simply says in the time domain what flat vs. frequency-selective fading said in the frequency domain.
Another aspect of wireless communication, different from the above, is the concept of how fast things are changing in the wireless channel. In the time domain, that aspect is referred to as time dispersion and is measured by coherence time; the coherence time describes how fast the wireless channel is changing. That aspect is important for estimating the quality of communication; for instance if the channel has a certain property, how long can we count on it? This defines for instance how often training sequences should be sent to estimate the wireless channel.
In the frequency domain the effect is best described by the Doppler spread: it describes how fast transmitter, receiver, and scatterers in-between are moving; the faster they are moving, the faster the wireless channel changes, and the more Doppler shift will be present. The instantaneous Doppler shift depends on the wave frequency and the maximum radial speed of the many scatters within the wireless channel; with a radial speed vr and wave incident at an angle θ:
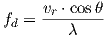 | (4.10) |
Doppler shift distribution varies, but an approximation of the maximum shift is simply: fm = vm∕λ, where vm is the maximum speed of the mobile (and λ the wavelength of the signal). And the Doppler spread is defined as twice the maximum Doppler shift: BD = 2fm, since the shift can be positive or negative depending on the direction of the motion.
| Doppler | Parameter | Symbol |
| Frequency domain | Channel impulse response | H(f) |
| Doppler spread | BD = 2fm | |
| Time domain | Channel impulse response | H(t) |
| Coherence time (50%) | Tc ≈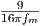 |
|
| Practical rule of thumb | Tc ≈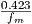 |
|
Fast or slow fading Depending on the values of these above parameters and how they compare to the length of transmitted symbol, the wireless channel will have fast fading (faster than a transmitted symbol) or slow fading (one or several transmitted symbol during a fade). This is of course a time domain interpretation describing how fading time compares to transmitted symbol time.
High or low Doppler Again depending on the values of the above parameters and how they compare to the speed of transmitted symbol, the wireless channel is said to have high or low Doppler spread. This simply expresses in the frequency domain what fast vs. slow fading said in the time domain.
It is important to understand the non-intuitive equivalence: for a given transmission rate, slow fading means long fades, meaning high coherence time, therefore low Doppler spread.
Wireless engineers might talk about fast fading meaning all of the above types of small-scale fading, simply because its variations are large over a small distance; this however should be avoided, instead always refer to it as small-scale fading (as it might be fast or slow).
It is important to reiterate the difference between the types of fading presented in the previous two section, and to understand that the characteristics presented in these two sections are completely uncorrelated. A wireless channel can be fast or slow and flat or frequency-selective. In either case, parameters above have to be compared to the transmitted symbol period (in the time domain) or to the data symbol baseband frequency (in the frequency domain).
To summarize, remember the following:

One more important aspect of the wireless channel and its small-scale fading deals with the distribution of angle of incidence to the receiving antenna. It is also referred to as angle of arrival. The RMS spread for angle of arrival has an impact on the statistical diversity of the received signal, which is important for instance in MIMO systems. The dual of angular spread is the coherence distance (see for instance reference [[140]], p. 68).
Small-scale fading is caused by different reflections of the signal (delayed, frequency shifted, constructive or destructive) and is usually modeled by a random variable with a certain probability distribution.
Rayleigh Rayleigh fading channels are widely used in theoretical approaches as well as in empirical urban studies. They are generally accepted to model multipath environments with no direct line of sight (LOS).
Given two random variable x and y Gaussian and zero-mean, that represent
some central limit theorem of a large number of multipaths (practically more
than six), it is shown that the signal envelope or amplitude α = 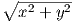 is
Rayleigh distributed [8]. This means that the channel amplitude follows the
Rayleigh distribution:
is
Rayleigh distributed [8]. This means that the channel amplitude follows the
Rayleigh distribution:
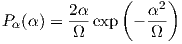 | (4.11) |
where Ω = is the mean square value of the random variate α.
The signal power is then related to α2. When the noise spectral density N0 is assumed to be one-sided Gaussian, the SNR has exponential distribution [78]: let us use as a measure of signal to noise ratio, SNR: γ = α2Es∕N0
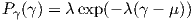 | (4.12) |
with γ ≥ 0, and λ = 1∕E(γ).
We can estimate the parameter λ for the exponential distribution in some way, such as by matching the first two moments with sample data {Xi}, of mean mX and standard deviation σX.
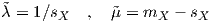 | (4.13) |
Rice
The amplitude of a fading channel may have a dominant component; the
faded amplitude is now given by α = 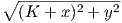 . Its probability
distribution is given by the Ricean distribution:
. Its probability
distribution is given by the Ricean distribution:
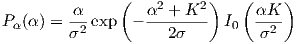 | (4.14) |
where I0(z) is the modified Bessel function of the first kind of order zero. That channel model offers the advantage of having an additional parameter K that has a physical meaning; but the Bessel function makes its computationally difficult, and has no straightforward form for its power or SNR.
Nakagami-m Similarly a Nakagami-m fading channel is often used for fade channels:
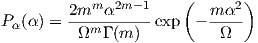 | (4.15) |
α ≥ 0, the SNR then follows the distribution [8][78]:
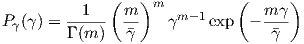 | (4.16) |
γ ≥ 0, which is gamma distributed. The problem of estimating parameters is more complicated in this case (as discussed in [79]ch. 17.7). Still, moment matching estimates lead to:
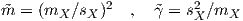 | (4.17) |
Gaussian Although not usually used for fading, the normal (or Gaussian) distribution is given for comparison:
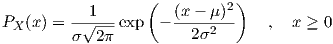 | (4.18) |
for which we may use the following simple estimates:
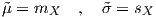 | (4.19) |
The estimate for 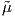 is unbiased and corresponds to moment matching and
maximum likelihood, and with large enough sample size the estimate for
is unbiased and corresponds to moment matching and
maximum likelihood, and with large enough sample size the estimate for 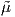 although biased is usually a good estimate.
although biased is usually a good estimate.
Log-normal There is a general consensus that large-scale fading may be approximated by lognormal distributions [17]. Its probability distribution is:
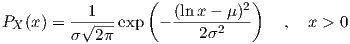 | (4.20) |
for which, the best estimates are simply obtained by change of variable Y = lnX and referring to the Gaussian case. A more complex approach would be to investigate Z = ln(X - Θ) but these estimations are more difficult and in many cases rather inaccurate ([79] ch. 14).
Weibull The flexibility and relative simplicity of Weibull distribution may also be convenient and leads to good data fit [80]:
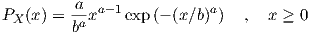 | (4.21) |
To estimate parameters, the simplest approach is to follow Weibull’s method based on the first two moments about the smallest sample value [79]ch. 21.
The above probability distributions are useful for modeling fading in wireless channels. In some cases empirical measurements are taken, and finding the fading situation may be a difficult problem. We look in this section at a specific case of fading in urban cores, and measure different events.
Test drives are conducted throughout major US cities in which mobile handsets continually place calls on several major cellular service providers. For that purpose a van is outfitted with several handsets, each cabled to a roof antenna, these antennas are placed as far as physically possible from one another to limit interferences. A system is setup to place a 90-second call on every handset, then remain idle for 30 seconds, and repeat the cycle. A wealth of data may be analyzed and compared; in particular we focus presently on the occurrence of dropped calls and call setup failures.
In this example we collect the rates of dropped calls and setup failures for major cities and service providers by driving between 1000 miles and 1500 miles (depending on the size of the city) on every major road and a portion of secondary roads. The data collected for dropped calls and setup failures is summarized in table 4.4.
| Moment of sample | Dropped Calls | Setup Failures |
| Mean (m) | mX(DC)= 1.32% | mX(SF)= 2.32% |
| Standard Dev. (s) | sX(DC)= 1.44% | sX(SF)= 2.67% |
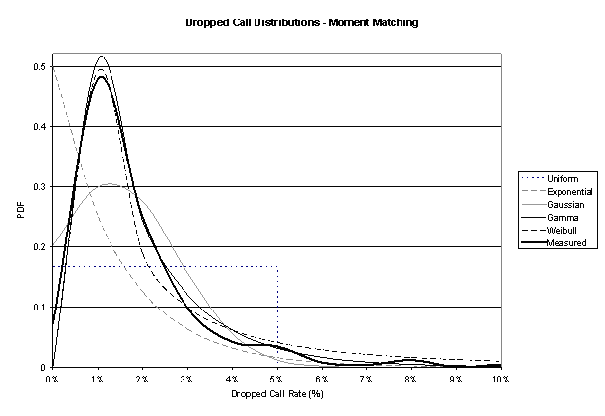
Moment matching for the above probability density distributions lead to table 4.5.
| Estimated | Parameters for | Parameters for |
| Distribution | Dropped Calls | Setup Failures |
| Uniform | b - a=0.0500 | b - a=0.0925 |
| Exponential | λ=69.2761, μ=-0.0012 | λ=37.4559, μ=-0.0035 |
| Gamma | a=0.8383, b=0.0158 | a=0.7542, b=0.0307 |
| Gaussian | μ=0.0132, σ=0.0144 | μ=0.0232, σ=0.0267 |
| Lognormal | μ=0.0130, σ=0.0140 | μ=0.0230, σ=0.0255 |
| Weibull | a=0.38, b=0.0022 | a=0.53, b=0.0150 |
A simple error estimate may be used to estimate differences between measured data and the different probability distribution functions covered above. The best fit (minimal error) is that of the gamma distribution; graphical representations also show a good fit.
Important correlation properties of fading deserve a closer look, both for large scale, and for small scale fading.
We’ve seen that Shadowing is modeled by a lognormal, zero-mean random variable; and that its standard deviation (in dB) relates with Jakes’ equation to service availability. But shadowing is largely caused by large obstacles, and is therefore correlated over fairly large distances. This is usually modeled with an autocorrelation function of the received signal r(d), a random variable varying (in space) with distance d from the transmitter; the autocorrelation function ρ(δ) is defined as the moment of the product of signals separated by δ. Sometimes the definition of the autocorrelation function divides by the variance (square of the standard deviation) in order to normalize the function between zero (uncorrelated) and one (perfectly correlated) signals:
![2
ρ(δ) = E [r(d) ⋅r(d + δ)]∕σ](classweb130x.png) | (4.22) |
(We use this normalized definition in this text.)
Shadowing autocorrelation often uses Gudmundson’s model [82], which approximates autocorrelation with an exponential decay, leading to the expression:
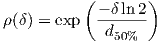 | (4.23) |
where d50 is the 50% correlation distance. The paper also cites measured values for suburban macrocell: normalized correlation is ρ = 0.82 at 100m for measurements made at fc = 900 MHz; and urban microcell: ρ = 0.3 at 10m and fc = 1.7 GHz.
Other models offer a two-dimensional approach to model the correlated shadowing that may occur in any direction of motion [83].
Further correlations exist between shadowing and other parameters:
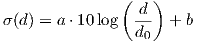 | (4.24) |
where d0=1m is a reference distance, a = 1.48 dB, b = -14.44 dB.
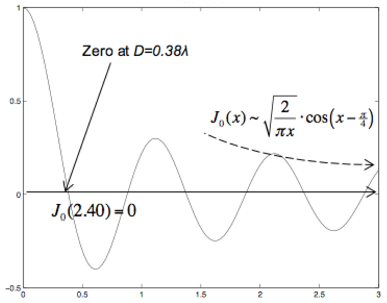
Diversity is related to de-correlation between paths. To measure path correlation, we define the autocorrelation of a signal, and examine how it changes in space. A classic autocorrelation model by Clarke or Jakes is often used to illustrate how a received signal changes at a different location (say at a distance D away) – [3] ch. 3 p. 65, [76]. With a number of assumptions, including a large (infinite) amount of scattering near the receiver, Jakes develops a convenient and realistic approximation model: ρ(τ) = J0(2πτfD), where J0 is the Bessel function of zero order, and fD is the Doppler shift. This leads to a correlation between paths to diversity antennas of: ρ(d) = J0(2πd∕λ), where d is the antenna separation (λ is the wavelength).
The optimal antenna separation is at the Bessel function’s first zero,
J0(2.40) = 0 at D = 0.38λ, which is often approximated to half a wavelength.
Also note that correlation decreases with (and is better than) the square root of
the separation D∕λ, since for large arguments J0(x) ~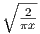 cos(x - π∕4).
cos(x - π∕4).
Recall here that the autocorrelation function is related to power spectral density by Fourier transform. The spectral density of the Clarke faded signal is therefore the Fourier transform of the Bessel function seen above:
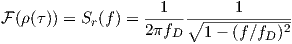 | (4.25) |
The value of de-correlation between paths lies in the diversity gain achieved when combining these paths. [76] mentions an often quoted result that correlation coefficient should be below 0.7 to achieve good diversity gain. [89] shows that 20λ horizontal separation (or 15λ vertical) leads to de-correlation greater than 0.7 for 93% of the measurements, and so recommends that as acceptable spacing between antennas (though it is much less for lower base station antenna heights as reported above). The paper goes on to estimate diversity gain as a function of correlation, for different diversity schemes:
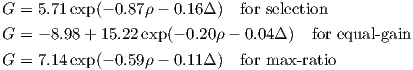 | (4.26) |
where G is the diversity gain at 90% signal reliability (in dB), Δ is the mean signal level difference between paths, and ρ their cross-correlation. Diversity gain varies with mean signal difference (the closer the signal levels, the better the diversity gain), cross-correlation, and of course combining schemes.
Assume that a call is dropped if the power received by all base stations is below a minimal power Pmin = -110dBm. Assume that the system initiates handoff when base station B1 power drops below PHO = -108dBm. The time required to complete the handoff is Δt=4s.
Question: above what speed vmax of the mobile would the call be dropped?
line | Parameter name | value | unit | Comments |
a | eNB transmit power | 17.4 | dBm | per Resource block |
b | eNB antenna gain | 10.0 | dBi |
|
c | EIRP | ? | dBm | per RB |
d | Body loss | 0.0 | dB |
|
e | UE antenna gain | 0.0 | dBi | For three sectors |
f | kT0B | -122.2 | dBm | Noise floor per RB |
g | UE noise figure | 8.0 | dB | Total system NF |
h | Required SNR | 21.0 | dB | For 64QAM |
i | System sensitivity | ? | dBm | ? |
j | Shadow margin | 8.0 | dB | Increases edge coverage |
k | Interference margin | 2.0 | dB | Due to load |
l | Maximum path loss | ? | dB | ? |
When the elevation angle α changes, slant path attenuation varies since the thickness of the atmosphere traversed by the radio link increases. That slant path attenuation is usually approximated by the cosecant law:
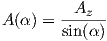 |
(Values are not in dB in the above equation).
Let us consider a system like Globalstar, operating at 1.6GHz, with satellites 1400km above ground, and with a rotation period of approximately 2 hours. (Also remember the average earth radius is approximately 6350km).
 | (4.27) |
Assume the following values:
What is the noise floor of that conventional cdmaOne base station?
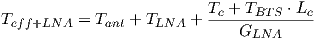 | (4.28) |
Assume the same values as above, and:
What is the noise floor of that system with LNA?
Copyright ©2019 Thomas Schwengler. A significantly updated and completed 2019 Edition is available.